初二數學勾股定理知識點,勾股定理公式及證明方法
時間:2023-06-24 10:04:38來源:考試幫手網作者:敏敏
初中數學的學習中,我們接觸到最重要的知識點就是勾股定理了,可以說勾股定理是中考必考之一,所以大家如果有參加中考的,一定要熟知勾股定理相關知識點,下面我們來看看到底什么是勾股定理,勾股定理的公式是什么?

勾股定理在幾何學中的實際應用非常廣泛。勾股定理,是幾何學中一顆光彩奪目的明珠,被稱為“幾何學的基石”。勾股定理即在任何一個平面直角三角形中的兩直角邊的平方之和一定等于斜邊的平方。在△ABC中,∠C=90°,則a²+b²=c² 。
如圖示,四邊形ACBD是直角梯形,AB之間有一點E,且AD=BE=b,AE=BC=a,CE=DE=c;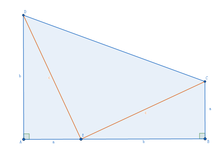
∴S ABCD = ½ (a+b)×(a+b) = ½ (a+b)² S△ADE=S△BCE=½ ab,S△CDE=½ c²
∴S ABCD =S△ADE+S△BCE+S△CDE=½ ab+½ ab+½ c²
∴½ (a+b)² = ½ ab+½ ab+½ c² (a+b)²=2ab+c² a²+b²+2ab=2ab+c²
∴ a²+b²=c²
平面向量法證明:
已知:△ABC中,∠C=90°。
求證:a²+b²=c²。
證明:設向量a為由點C指向點B的向量,b為由點C指向點A的向量,c為由點A指向點B的向量,則c=a-b。
于是c²=(a-b)²=a²+b²-2a·b=a²+b²-2abcosC=a²+b²。
平面向量法表明,勾股定理是余弦定理的特殊形式(當∠C為90°時,cos C=0)。
例題:今有池,方一丈,葭生其中央,出水一尺,引葭赴岸,適與岸齊,問水深、葭長各幾何?用現代語言表述如下:有一個正方形的池塘,池塘的邊長為一丈,有一棵蘆葦生長在池塘的正中央,并且蘆葦高出水面部分有一尺,如果把蘆葦拉向岸邊則恰好碰到岸沿,問水深和蘆葦的高度各多少?(1丈=10尺。) 解:設葭長x丈。
依題意,由勾股定理得(10÷2)²+(x-1)²=x²,解得x=13,則x-1=12。
答:水深12尺,葭長13尺。

勾股定理在幾何學中的實際應用非常廣泛。勾股定理,是幾何學中一顆光彩奪目的明珠,被稱為“幾何學的基石”。勾股定理即在任何一個平面直角三角形中的兩直角邊的平方之和一定等于斜邊的平方。在△ABC中,∠C=90°,則a²+b²=c² 。
如圖示,四邊形ACBD是直角梯形,AB之間有一點E,且AD=BE=b,AE=BC=a,CE=DE=c;

∴S ABCD = ½ (a+b)×(a+b) = ½ (a+b)² S△ADE=S△BCE=½ ab,S△CDE=½ c²
∴S ABCD =S△ADE+S△BCE+S△CDE=½ ab+½ ab+½ c²
∴½ (a+b)² = ½ ab+½ ab+½ c² (a+b)²=2ab+c² a²+b²+2ab=2ab+c²
∴ a²+b²=c²
平面向量法證明:
已知:△ABC中,∠C=90°。
求證:a²+b²=c²。
證明:設向量a為由點C指向點B的向量,b為由點C指向點A的向量,c為由點A指向點B的向量,則c=a-b。
于是c²=(a-b)²=a²+b²-2a·b=a²+b²-2abcosC=a²+b²。
平面向量法表明,勾股定理是余弦定理的特殊形式(當∠C為90°時,cos C=0)。
例題:今有池,方一丈,葭生其中央,出水一尺,引葭赴岸,適與岸齊,問水深、葭長各幾何?用現代語言表述如下:有一個正方形的池塘,池塘的邊長為一丈,有一棵蘆葦生長在池塘的正中央,并且蘆葦高出水面部分有一尺,如果把蘆葦拉向岸邊則恰好碰到岸沿,問水深和蘆葦的高度各多少?(1丈=10尺。) 解:設葭長x丈。
依題意,由勾股定理得(10÷2)²+(x-1)²=x²,解得x=13,則x-1=12。
答:水深12尺,葭長13尺。
相關推薦

-
1公頃等于多少米,數學單位換算表大全
初中階段,我們就接觸到個中單位換算,單位換算是數學中非常重要的一個內容,比如你知道1公頃等于多少米嗎

-
二次函數的圖像和性質?二次函數中考壓軸題
二次函數是初中數學中非常重要的一個知識點,2020年中考馬上就要到了,不知道大家對于二次函數的知識點有沒

-
初中數學根號怎么算,常用根號值表
初中數學中,我們在學習到根號這一內容時,大家有沒有很吃力呢?如果你感覺根號比較難懂的話,那么,可能就

-
等腰三角形知識點總結,等腰三角形面積公式
初中數學中,幾何圖形是大家學習數學最難、也是最重要的一個點,特別是等腰三角形的相關知識點是高頻考點,

-
初中數學知識點總結,初中數學定理公式大全
初中階段的數學雖然并不是很難,但是知識點是非常多的,特別是數學公式及定理是非常多的且容易混淆的,很多

-
高中幾何不好怎么辦?高中數學幾何解題技巧
數學這門學科,一直都是最讓人頭疼的學科之一。在高中想要在數學上取得不錯的成績就得名卻直接的強勢和弱勢