高中幾何不好怎么辦?高中數學幾何解題技巧
時間:2023-06-24 10:04:38來源:考試幫手網作者:大白
數學這門學科,一直都是最讓人頭疼的學科之一。在高中想要在數學上取得不錯的成績就得名卻直接的強勢和弱勢,將各個重點難點逐一擊破才是最好的方法。今天就讓我們一起來看看關于高中數學幾何解題技巧。

想要掌握高中幾何,一個良好的空間想象能力還有突破思維上的局限性是學好幾何的關鍵,再者學習數學還需要一定的嚴密性和邏輯性,在這些基礎上加以學習和理解,才能讓你更好的了解幾何的世界。
幾何世界中最讓人難以琢磨的就是立體幾何了,一般情況下立體幾何會考察的知識點主要就是下面這幾種:
立體幾何經常考察的知識點主要就是下面這幾種
一、兩個平面平行的主要性質:
由定義知:“兩平行平面沒有公共點”。
兩個平面平行的性質定理:“如果兩個平行平面同時和第三個平面相交,那么它們的交線平行”。
而在解這些立體幾何的問題目時經常會用到輔助線,輔助面和法向量這些基本的技巧
二、判定兩個平面平行的方法:
根據定義——證明兩平面沒有公共點;
判定定理——證明一個平面內的兩條相交直線都平行于另一個平面;
證明兩平面同垂直于一條直線。
三、平行與垂直的問題
應該是大家最常遇到了幾何題型了,但它也是最基礎的一個題型,大家可以利用線線平行(垂直)、線面平行(垂直)、面面平行(垂直)相互轉化的思想來解決問題。
在試卷中,如果幾何出現在選擇填空題中大部分都是考核你的邏輯推理型問題,解答題考核的是計算能力,大家一定要靈活借用輔助面和輔助線,然后就是要多做題,累計經驗,相信時間一久,幾何對你來說一定不會太難了。

想要掌握高中幾何,一個良好的空間想象能力還有突破思維上的局限性是學好幾何的關鍵,再者學習數學還需要一定的嚴密性和邏輯性,在這些基礎上加以學習和理解,才能讓你更好的了解幾何的世界。
幾何世界中最讓人難以琢磨的就是立體幾何了,一般情況下立體幾何會考察的知識點主要就是下面這幾種:
立體幾何經常考察的知識點主要就是下面這幾種
一、兩個平面平行的主要性質:
由定義知:“兩平行平面沒有公共點”。
兩個平面平行的性質定理:“如果兩個平行平面同時和第三個平面相交,那么它們的交線平行”。
而在解這些立體幾何的問題目時經常會用到輔助線,輔助面和法向量這些基本的技巧
二、判定兩個平面平行的方法:
根據定義——證明兩平面沒有公共點;
判定定理——證明一個平面內的兩條相交直線都平行于另一個平面;
證明兩平面同垂直于一條直線。
三、平行與垂直的問題
應該是大家最常遇到了幾何題型了,但它也是最基礎的一個題型,大家可以利用線線平行(垂直)、線面平行(垂直)、面面平行(垂直)相互轉化的思想來解決問題。
在試卷中,如果幾何出現在選擇填空題中大部分都是考核你的邏輯推理型問題,解答題考核的是計算能力,大家一定要靈活借用輔助面和輔助線,然后就是要多做題,累計經驗,相信時間一久,幾何對你來說一定不會太難了。
相關推薦

-
中專和高中有什么區別,中專文憑和高中文憑一樣嗎哪個好
眾所周知,初中中考是一道比例非常大的分流如果順利通過就會進入高中進行學習,而沒有順利通過要么就輟學要

-
高中生網上補習靠譜嗎?高中生網上補課平臺哪個好
多年的發展教育行業依舊是全國人民都非常重視的方面,而隨著當下的多年發展線下輔導班已經成為嚴禁和打擊的

-
湖南十大名校中學排名2023,湖南四大名校高中是哪幾所
湖南作為幸福感非常強烈的省份,在美食、美景以及教育等方面都有著比較優質的基礎,比如大學、高中、初中都

-
合肥中學排名 合肥最好的高中是什么?
好的高中對于高考成績是有很大的影響的,所處的環境是很容易改變一個人的,所以才有歷史上孟母三遷的故事,

-
2023年上海高中排名一覽表,上海市重點高中有哪些?
高中學校的好與不好可能影響著孩子上學的成績,很多家長都想讓孩子能夠考上當地最好的高中學校,要想報考好
-
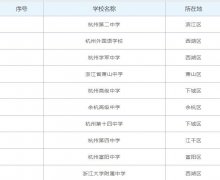
杭州高中學校排行榜,杭州最好的重點高中有哪些?
隨著社會的進步,家長們越來越對孩子的教育加以重視了,很多家長想盡一切辦法讓孩子上一個好的重點高中學校